Tempo stimato di lettura: 14 minuti
Ogni giorno in azienda si devono prendere decisioni. Queste decisioni arrivano tipicamente dall’analisi di complessi database, fogli Excel, quindi numeri che si trasformano in grafici, tabelle, tabelle aggregate (pivot), KPI, etc.. Dalla comparazione sistematica (o benchmarking) di questi risultati si motivano quindi razionalmente le scelte.
E se questi risultati fossero sbagliati? Può accadere. Tuttavia siamo in grado di mitigarne il rischio, procedendo con ripetuti controlli sulla qualità della base dati e sulle formule matematiche utilizzate.
Cosa accadrebbe invece se non fossimo consci di commettere degli errori di interpretazione dei risultati (seppur matematicamente corretti e basati su dati qualitativamente validi)?
Il Lean Six Sigma (LSS) fornisce gli strumenti per leggere i numeri in modo differente. Ci fa indossare un paio di occhiali speciali, quelli usati dalla statistica, che non usiamo mai (per motivi culturali o per pigrizia). Vediamo come ci può aiutare e perché.
(L’argomentazione trattata di seguito tiene conto soltanto di aspetti di significatività statistica e non sostanziale o fisica. Inoltre non sono considerate le problematiche legate all’errore beta).
La misura
Obiettivo del LSS è di curare processi malati. Per fare questo serve essere sicuri che il malato lo sia per davvero. Quindi, una volta studiato il processo in Ring/Scope (cioè pertinente al fenomeno da analizzare), si procede con l’identificazione degli elementi chiave (quindi le X, o cause potenziali) da sottoporre per la misura della Y (variabile effetto).
Quando si parla di misura ci si scontra tipicamente su queste domande:
- Cosa misuro? Ovvio (ma non banale), scelgo opportunamente le mie X da legare alla Y
- Come misuro? Ovvio (ma non banale), utilizzo strumenti di misura adeguati, verificati (tarati) e utilizzati da personale addestrato. Se il dato fosse già disponibile, mi preoccuperei di verificare che, quanto in mio possesso, rispecchi i requisiti ottimali di misura
- Dove misuro? Ovvio (ma non banale), effettuo/filtro misure attinenti i soli processi interessati (in Ring/Scope)
- Quando misuro? Ovvio (ma non banale), effettuo/filtro misure attinenti un periodo temporale adatto ad identificare il problema (quando presente, ma anche quando non presente)
- Quanto misuro? Qui la risposta purtroppo non è immediata.
Immaginiamoci che il Cosa, il Come, il Dove e il Quando siano in qualche modo gestiti.
Quanto devo misurare? Cosa cambia se misuro tanto o poco? Come questo può cambiare le nostre decisioni?
Vediamo un esempio.
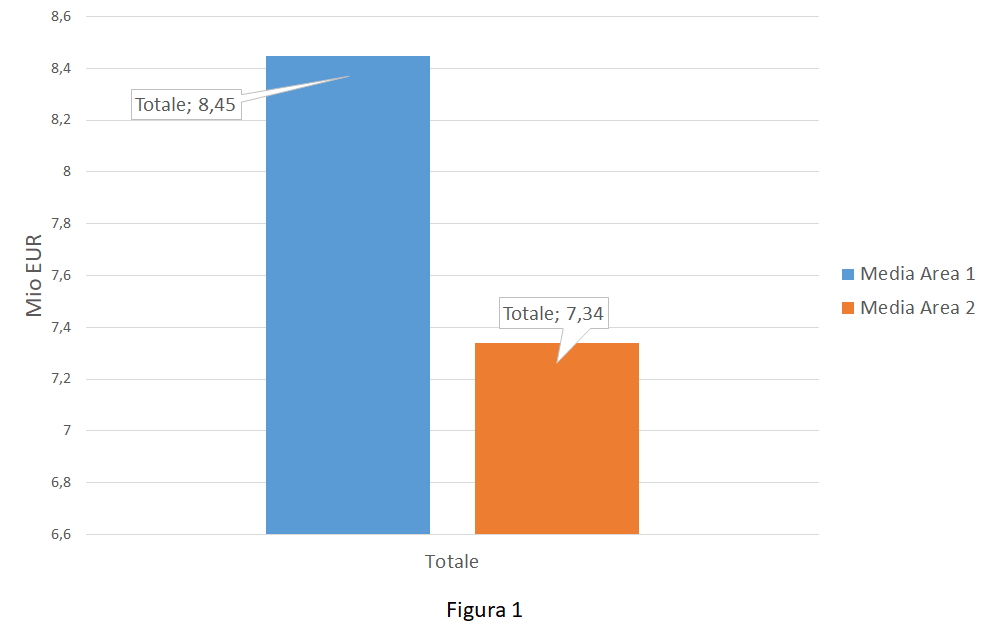
Immaginiamoci di visualizzare un diagramma fatto in Excel sulle performance di vendita della mia azienda che produce pennarelli. Nello specifico si è deciso di mappare 2 campioni afferenti le vendite in Area 1 e in Area 2 nei primi 3 mesi dell’anno (valori normalizzati per abitante in Mio EUR).
Il management, visto il grafico (figura 1), propone di attuare immediatamente delle azioni correttive per rimettere in carreggiata l’Area 2, dal momento che questa fornisce prestazioni chiaramente insoddisfacenti rispetto l’Area 1.
Il LSS avrebbe suggerito di analizzare meglio la base dati. Si sarebbe scoperto che, molto probabilmente, le due aree performavano mediamente nello stesso modo (con un livello di confidenza del 95% o, dualmente, un errore del 5%) e che non c’era quindi da preoccuparsi. La decisione presa era dunque probabilmente inutile!
L’elemento chiave per comprenderne il motivo ricade nell’incertezza dovuta alla misura campionaria.
L’incertezza campionaria
La misura campionaria (o campionamento) dev’essere efficace in quanto deve fotografare al meglio un certo fenomeno (o popolazione) su cui si vorrebbe la massima confidenza dal momento che non se ne conosce la natura. Dovrebbe poi essere anche efficiente, poiché questa fotografia andrebbe fatta misurando il meno possibile (a costo minore).
Misurare troppo poco potrebbe condurre a:
- maggiore ambiguità nei risultati.
- rischio di underfitting (eccessiva genericità del modello).
Misurare troppo, al contrario, potrebbe provocare:
- costi elevati (lunghi tempi di acquisizione e di elaborazione).
- rischio di overfitting (insufficiente genericità del modello).
In sintesi, con il campionamento si vorrebbe raggiungere il seguente obiettivo: calcolare per singolo campione il numero n minimo (quindi ottimo) di misure che permetta di indagare il fenomeno originario Y (popolazione) con sufficiente confidenza.
Se il processo in esame si comportasse in modo deterministico (cioè sempre nella stessa maniera), impostando opportunamente le X, basterebbe un campione di dimensione pari a 1 per rappresentare la popolazione Y! Purtroppo non è così: persevera l’ineluttabile e non eliminabile variabilità del nostro universo. Questo fa sì che, per la pura legge del caso, nel medesimo stato S, stimolato nelle stesse modalità X, un evento produca risultati Y differenti. Di questo dobbiamo tenere conto.
Fissate le X sul processo, se si potessero prelevare idealmente nello stesso istante 2 campioni distinti di Y (aventi n=1 ciascuno), si troverebbero quasi certamente Y1 diverso da Y2. Quale delle due misure fornirebbe il dato “più corretto”, cioè più rappresentativo del fenomeno Y? Entrambi i valori scatterebbero una fotografia reale del processo (presupponendo misurazioni effettuate in condizioni ottimali). Idealmente nessuna delle due misure è più corretta dell’altra.
Se conoscessimo la “vera” misura di Y (che chiameremo YP) saremmo in grado di valutare l’errore di misura per Y1 e Y2. La formula Ei = |YP – Yi| con i = 1, 2 calcola lo scostamento di Yi da YP in valore assoluto. A questo punto saremmo in grado di scegliere il campione più accurato, cioè quello con errore Ei minore.
La misura reale YP di uno specifico fenomeno che si vorrebbe misurare è, in un processo stocastico, rappresentativa, per quel fenomeno, dell’evento più probabile. La statistica (definizione frequentista della probabilità) ci dice che la probabilità di un certo evento è legata alla frequenza relativa del verificarsi dell’evento stesso. Questa affermazione è tanto più vera quanto più sono numerose le misure per quell’evento. Dal momento che il numero di prove che si dovrebbero idealmente effettuare tenderebbero all’infinito, il valore rigoroso di YP non lo conosceremo mai!
Detto al contrario, dato Yi non sapremo mai dove si trova YP e quindi non sapremmo calcolare Ei. La scelta del campione più rappresentativo sarebbe lasciato al puro caso e non sarebbe basato su alcun razionale.
Invece di utilizzare un campione di 1 elemento, potremmo utilizzare 1 campione di dimensione n >>1. Il contenuto informativo ovviamente aumenta. Diversamente da prima, diventa necessario sintetizzare questo aumento di informazione in qualcosa di più sintetico.
A questo riguardo ci viene in aiuto la Statistica.
La statistica è una disciplina che ha come fine lo studio quantitativo e qualitativo di un particolare fenomeno collettivo in condizioni di incertezza o non determinismo, cioè di non completa conoscenza di esso o parte di esso.
Wikipedia
In particolare la Statistica Descrittiva ci suggerisce di sintetizzare n dati attraverso gli indicatori sintetici di tendenza centrale (es. media, mediana, moda), di dispersione (es. range, stdev, varianza) e di forma (es. skewness e kurtosis). Tutti questi valori non sarebbero calcolabili per n=1.
Purtroppo, anche utilizzando campioni più grandi, risulterebbero immutate le condizioni di prima sull’incertezza della misura. Es. data la media di un campione, non saremmo in grado di conoscere la media della popolazione da cui quel campione è stato estratto.
Tuttavia qualcosa è cambiato: all’aumentare di n e del numero di campioni utilizzati, si inizia ad apprezzare sempre più la validità del Teorema del Limite Centrale, teorema questo alla base della Statistica Inferenziale.
La Statistica Inferenziale, partendo dal valore sintetico di un campione (es. la media), permette di calcolare, con un certo livello di confidenza (es. 95%) o, dualmente, con un certo margine di errore (es. 5%), l’intervallo entro cui è possibile trovare quello stesso valore sintetico ma riferito alla popolazione (valore questo, come abbiamo detto prima, che rimane puntualmente ignoto). Questo intervallo si chiama Intervallo di confidenza (CI).
CI dipende principalmente:
- dal coefficiente di rischio di commettere un certo errore (alpha)
- dalla innata variabilità della popolazione (stdev)
- dalla dimensione del campione (n).
Ipotizzando costante alpha e stdev, all’aumentare di n, CI diminuisce.
In figura 2 si può vedere come cambia CI (=Ux – Lx) con riferimento alla media (x) di un certo fenomeno aleatorio, campionato per n=10, n=100, n=1000. Il valore medio puntuale della popolazione (qui pari a 5, noto solo per motivi didattici) attraversa tutti gli CI.
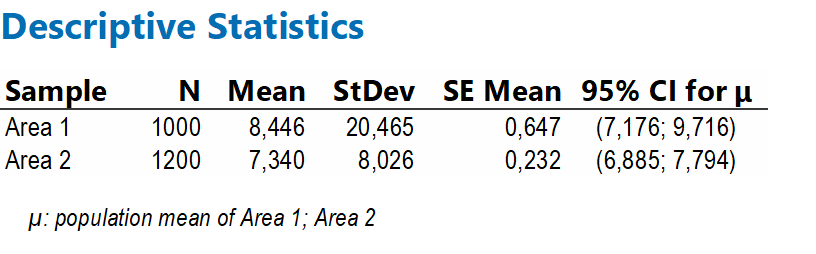
Si analizzino in dettaglio i valori di Area 1 e Area 2 (prima non utilizzati)
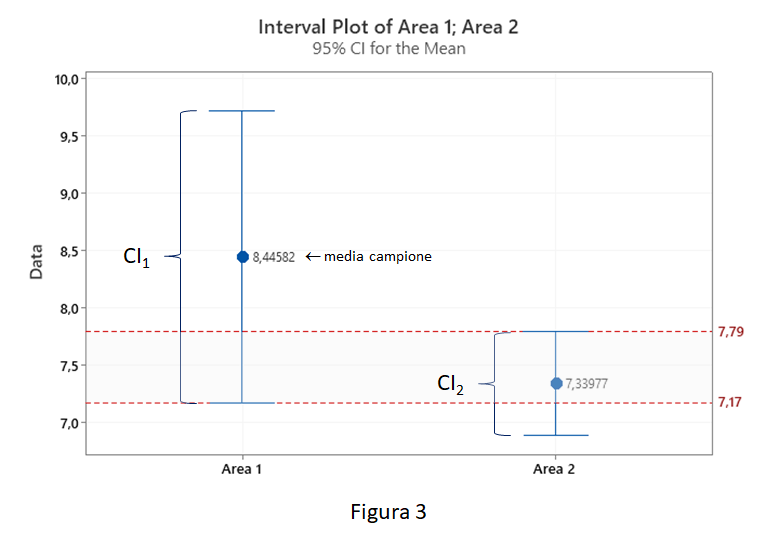
Con questi valori di n e stdev, avendo fissato il rischio alpha al 5%, siamo in grado di calcolare CI per la media dell’Area 1 e dell’Area 2. Si leggano i risultati in formato grafico attraverso l’Interval Plot (figura 3).
Si noti come CI parzialmente si sovrappongono. In particolare tra 7,17 e 7,79, Area 1 e Area 2 potrebbero condividere gli stessi valori di media della popolazione. Con una confidenza del 95% potremmo dunque affermare che, specificatamente per l’indicatore della media, i due campioni siano figli della stessa popolazione, cioè siano statisticamente simili!
Diventano adesso evidenti i motivi per cui, aumentando la dimensione del campione per l’Area 1 (n>>1200), il suo CI si sarebbe ridotto al punto che saremmo arrivati a conclusioni opposte (Area 1 e Area 2 sono davvero differenti).
Misurare tanto o poco, quindi, può far cambiare le nostre decisioni!
Conclusioni
I risultati numerici ci aiutano a prendere decisioni. Il loro valore è quindi strategico per l’azienda. Queste sintesi numeriche, che emergono a valle delle nostre analisi, sono basate su valori campionari.
Il campione per come è dimensionato (n), la popolazione per come è caratterizzata (stdev) e il coefficiente di rischio (alpha) stabiliscono l’incertezza della misura (Intervallo di confidenza). È questa incertezza che non sappiamo leggere. È questa incertezza che può farci cambiare idea.
LSS, utilizzando la statistica, ci insegna a gestire compiutamente i nostri numeri e, di conseguenza, oggettivare al meglio le nostre deduzioni.
Alla fine, quindi, chi performa meglio, il processo A o il processo B?